|
|
|
Zielgerichtete Variation von Trochoiden
|
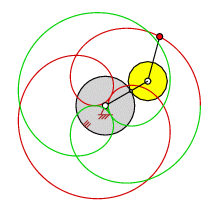
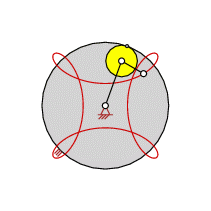
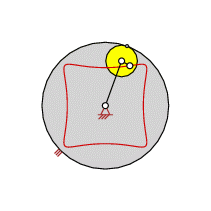
| Trochoide (zyklische Kurve) [Bild links] Koppelpunkt- bahn einer Doppelkurbel [Bild rechs] |
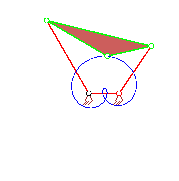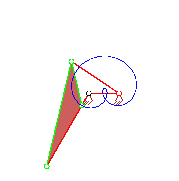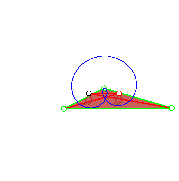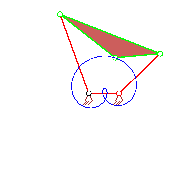
|

mit Hilfe von Gangpolkurve, BALLscher Kurve und Übergangskurve
- Möchten Sie eine Trochoide bzw. Zykloide zielgerichtet variieren?
- Wollen Sie Kurbelschwingen oder Doppelkurbeln berechnen?
- Wollen Sie Koppelkurven zielgerichtet variieren?
Es gibt zwar inzwischen sehr gute numerische Optimierungsalgorithmen, aber es Hilft ungemein, wenn analytischen Wissen über die Lösungsmenge bekannt sind.
- Trochoiden mit gesuchten Eigenschaften lassen sich schon mit wenigen Rechenschritten und einigen Proberechnungen
(z. B. mit den Algorithmen am Ende dieser verlinkten Seite) schnell finden
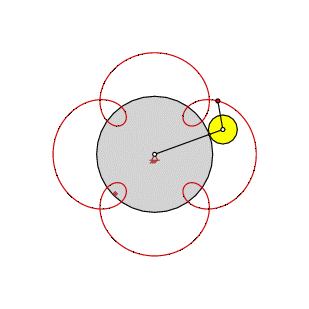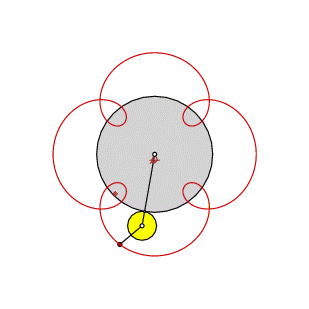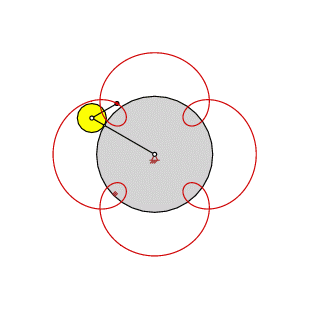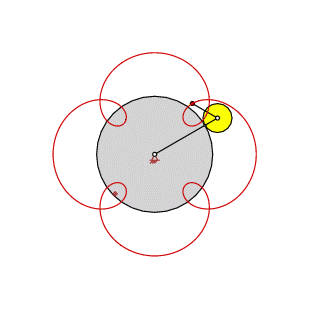
Als Beispiel wird hier ein Punkt gezeigt, der in 2 Umläufen des beweglichen Rades eine Trochoide mit 3 Schleifen erzeugt. (Detailliertere Informationen finden Sie hier.)
Variation einer Trochoide bzw. einer Zykloide
Zum Einstieg in die Erkenntnisse über die Variation einer Trochoide bzw. einer Zykloide- gibt es hier eine Übersicht über die Formenvielfalt der Epitrochoiden
- hier eine der Hypotrochoiden
- und hier eine phänomenologische Herleitung der Formenvielfalt von Epitrochoiden
- hier eine von Hypotrochoiden
- und hier geht es zur schiebergesteuerten Animation von Trochoiden
Freeware Programm DROMEG
Das Freeware-Programm DROMEG zum Berechnen und grafischen Animieren von Trochoiden sowie von viergliedrigen Gelenkgetrieben wird auf der Seite "Analyse-Programm" beschrieben.
Die Download-Seite zu dem Programm DROMEG finden Sie hier
Viergliedrigen Gelenkgetriebe
- Die Angabe zu den Bildern bezüglich der Eigenschaften von Kurven, die von Punkten erzeugt werden, die innerhalb der Begrenzungen durch BALLscher Kurve, Gangpolkurve und
Übergangskurve liegen, stammt übrigens von Untersuchungen der Koppelkurven von (viergliedrigen) Gelenktgetrieben.
Die Theorie dazu wird in meiner Dissertation beschrieben und kann mit Hilfe des Programms DROMEG nachvollzogen werden.
Trochoiden, Koppelkurven etc.
Die Grundlagen für die
- Zielgerichtete Getriebe-Analysen und
- Synthese von ebenen Koppelkurven ( Koppelpunktbahnen) sowie
- Variationmöglichkeiten von Trochoiden
entnehmen Sie bitte dem Getiebe-Lexikon,
daß sich beschränkt auf die Grundlagen meiner Dissertation:
- Einteilung einer eben bewegten Ebene in Felder
- mit qualitativ gleichen Koppelpunktbahnen
- unter besonderer Berücksichtigung der Übergangskurve
Wechsel zur Homepage meiner Dissertation
Anzahl der Besucher dieser Seite:

|
|